2-2. 重力
高知大学自然科学系 田部井隆雄
神奈川県温泉地学研究所 里村幹夫
京都大学大学院理学研究科 福田洋一
2-2-1. 地球の重力(*)
地球上にある物体に働く地球の万有引力と地球の自転による遠心力の合力を重力と呼び, 単位質量当りの重力を重力加速度と呼ぶ. 測地学では, 空間や時間で重力加速度がどのように変化するかを取り扱い, 質量の違いによる重力の違いは問題としない. そのため, 重力加速度のことを単に重力と呼ぶのが通例になっている. そこで, 重力の単位にも加速度の単位, $m/s^2$や$cm/s^2$を用いる. 現在では一般に, MKS単位系である$m/s^2$の使用が推奨されているが, 測地学では今でもCGS単位系が用いられることが多い. 特に, $cm/s^2$は, 物体の自由落下の速度がその質量に依存しないことを発見しピサの斜塔の故事(これは作り話だといわれている)で有名なガリレオ・ガリレイ(1564~1642)に因み, Gal(またはgal)と呼ばれ, 重力に関連した研究では, 広く用いられている(図1).
よく知られているように, 地球表面での重力は, 平均的に980Galである. もう少し詳しくみると, 地球の形が回転楕円体に近いこと, また, 自転による遠心力のため, 赤道上で約978Gal, 極で約983Galと, 緯度の違いにより最大約0.5%(5Gal)変化する(図2). このような緯度の違いによる重力の変化を補正したとしても, 地球内部の密度構造の違いなどにより, 地球上で重力は最大0.3Gal程度変化する. また, 同じ地点の重力も, 地球潮汐などにより, 時間的に最大0.0003Gal程度変化している. このような重力の空間的・時間的変化を表すのにGalは値が大きすぎて不便であるので, 通常, 空間的な重力の変化(重力異常)を表すためには, $1/1000(10^{-3})[Gal]$であるmGalを, また, 時間的な変化を表すためには, $1/1,000,000(10^{-6})[Gal]$であるμGalが用いられる.

図1. MKS単位系とCGS単位系の関係.
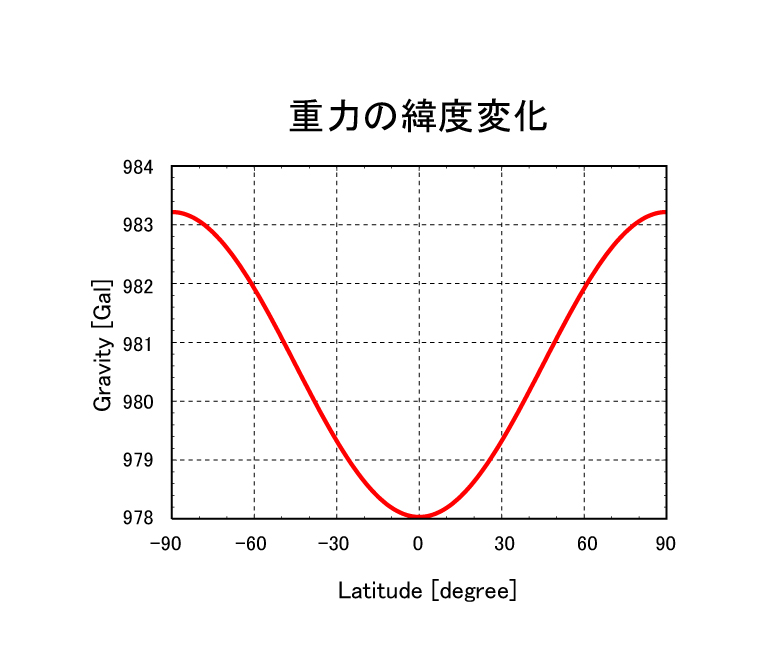
図2. 重力の緯度による変化.
2-2-1-1. 万有引力と遠心力(**)
質量$m_1$と$m_2$の2つの物体が距離$r$だけ離れてあるとき, これらの物体の間に次の式で表されるニュートンの万有引力(以下, 単に引力と呼ぶ)$F$が働く.
ここで$G$は万有引力定数で, $(6.673±0.010)×10^{-11} [m^{3}s^{-2}kg^{-1}]$である. 地球上にある質量を持つすべての物体と地球との間に引力が働いている.
\[ F=G\frac{m_1m_2}{r^2} \tag{1} \]
質量$m$の物体が, 半径$r$の円周上を角速度$\omega$で回転していると, $F=mr\omega^2$の遠心力が働く. 地球は自転軸のまわりに自転しているため, 地球上にある物体はすべて, 自転軸から遠ざかる方向に自転軸からの距離に比例した遠心力が働くことになる.
次に, 地球の引力と遠心力の大きさを見積もってみよう. 1kgの物体に働く地球の引力は, 地球半径が約$6.4×10^6 [m]$, 地球の質量が約$6.0×10^{24} [kg]$で, 全質量が地球中心にある質点と仮定すると, $(6.7×10^{-11})\times(6.0\times10^{24})/(6.4\times10^6)^2=9.8 [N]$となる. 1kgの物体に働く遠心力は, 遠心力が最も大きい赤道上で$1×(6.4×106)×(7.3×10^{-5})2=3.4×10^{-2}[N]$となる. つまり赤道上では地球自転の遠心力の大きさは地球の引力の0.3%強となる. 先に, 極と赤道での重力の差は, 約0.5%であると述べたが, 遠心力の影響だけではその差は生じない. この違いは, 実際の地球の形がほぼ回転楕円体であるのに, 上の計算では, それを無視したことによる.
地球の引力の大きさを実感するために, この物体の1m横に1トンの物体があるとしてその引力を求めると, $(6.7\times10^{-11})\times(1\times10^3)/ 12 = 6.7×10^{-8}[N]$となる. これは, 地球全体の引力に比べ, 僅か10億分の7(7μGal)程度の大きさである.
2-2-1-2. 回転する球の重力ポテンシャル(***)
引力$F$が働いている物体を, 引力と反対の方向$dr$だけ移動させたとすると, 物体に対して$-F\cdot dr$の仕事をしたことになり, その物体は$-F \cdot dr$のエネルギーを得る. このようにして得たエネルギーは, 物体の位置にのみ依存するので, 位置エネルギーと呼ばれる. また, 単位質量あたりの位置エネルギーを表す関数$V(r)$をポテンシャルと呼ぶ.
地球が球対称であると仮定すれば, その引力は全質量$M$が球の中心にある質点の引力と同じになり, 中心から$r$の地点の単位質量に働く引力$F$は, $F =\frac{GM}{r^2}$となる. このとき, $r$を$dr$ だけ移動させたときの位置エネルギーの変化は, $-GM\frac{dr}{r^2}$である. したがって, 位置エネルギーを表す$V(r)$は,
\[ V(r)=-\int F dr = -GM \int \frac{dr}{r^2} = \frac{GM}{r} \tag{2} \]
であり, $V(r)$を引力ポテンシャルと呼ぶ. なお, (2)式では, 無限遠で$V(r)$が$\theta$となるように積分定数を決めている.
次に, 遠心力のポテンシャル$\Phi$を考えると, 赤道上での単位質量に働く遠心力は外向きに$F =r\omega^2$であり, 遠心力は地球の中心で0であるので, $F\cdot dr$を地球の中心から地表面まで積分することで,
\[ \Phi = \int r\omega^2 dr =\frac{1}{2} \omega^2 r^2 \tag{3} \]
となる. 同様に, 地心緯度$\phi$での遠心力のポテンシャルは, 遠心力$F=r\omega2\cos\phi$に$dr$の遠心力方向の成分$\cos{\phi} \cdot dr$ を掛けて積分することにより,
\[ \Phi = \int r \omega^2 \cos \phi \cdot \cos \phi dr = \frac{1}{2} \omega^2 r^2 \cos^2 \phi \tag{4} \]
となる.
力(または加速度)はベクトル量であるので, 引力と遠心力を足し合わせる際にはその方向を考慮する必要があるが, ポテンシャルはスカラー量であるので, 単純な足し算でよい. すなわち, 重力ポテンシャルは, 引力ポテンシャルと遠心力ポテンシャルの和として与えられる.
球対称な地球の重力ポテンシャル$U$は,
\[ U=V+\Phi=\frac{GM}{r}+\frac{1}{2}\omega^2 r^2 \cos^2 \phi \tag{5} \]
となる.
2-2-1-3. 回転する球の重力(***)
重力の方向と重力ポテンシャルの関係について考えてみよう. 重力ポテンシャルによる位置エネルギーは, ある物体を重力$F$の方向に沿って移動させた場合に変化する. このことは, 重力ポテンシャルが一定の面(等重力ポテンシャル面)内では接線方向の重力の成分はゼロ, あるいは, 重力の方向は等重力ポテンシャル面と直交していることを示している. 次に, 重力の大きさと重力ポテンシャルの関係であるが, 重力が大きい時, それに逆らって僅かな距離を移動させるだけで重力ポテンシャル(位置エネルギー)は大きく変化する. すなわち, 重力の大きさは重力ポテンシャルの空間的な変化率に比例している.
一般に, あるスカラー量の空間的な変化率は, 勾配(gradient)と呼ばれる空間の偏微分係数を成分に持つベクトルで与えられ, 重力$F$ は重力ポテンシャル$U$の勾配として次式で表される.
\[ F=\mathrm{grad} U = \left( \frac{\partial}{\partial x}\boldsymbol{i} + \frac{\partial}{\partial y}\boldsymbol{j} + \frac{\partial}{\partial z}\boldsymbol{k} \right) U \tag{6} \]
ただし, $\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}$は, $x,y,z$成分方向の単位ベクトルである.
次に, 回転している球の重力を求めてみよう. (5)式の回転している球の重力のポテンシャルは,
\[ U=\frac{GM}{r}+\frac{1}{2}\omega^2r^2\cos^2\phi \tag{7} \]
であり, 球座標での勾配の$r$(動径方向)成分は, $\partial/\partial r$ , $\phi$(緯度方向の接線)成分は, $(1/r) \cdot (\partial /\partial \phi)$であるので, それぞれ, 重力の$r$成分$\gamma_r, \phi$成分$\gamma_\phi$は,
\[ \begin{equation} \begin{array}{l} \gamma_r=\frac{\partial U}{\partial r}=-\frac{GM}{r^2}+r\omega^2 \cos^2 \phi \\ \gamma_\phi=\frac{1}{r}\frac{\partial U}{\partial \phi} = -r \omega^2\cos\phi\sin\phi \end{array} \end{equation} \tag{8} \]
となる.
ここで注意すべきは, 回転する球では遠心力の影響により, $\phi$が0度(赤道)または90度(極)以外では, 重力の接線成分$\gamma_\phi$がゼロにはならないこと, すなわち, $r$方向(動径方向)と重力の方向は一致しないことである. 言い換えると, 回転する球の表面は, 重力の等ポテンシャル面にはならないことである.
2-2-1-4. 地球楕円体の重力(***)
地球の形は回転楕円体に極めて近いので, 実際の地球の重力を近似する方法としても回転楕円体の重力を用いるのが都合がよい. このように, 実際の地球の形ならびに重力場の近似として用いる回転楕円体を地球楕円体と呼び, 球の場合と異なり, その表面は, 重力の1つの等ポテンシャル面となる.
地球楕円体のように, 回転している楕円体の重力ポテンシャル, あるいはその重力を求めることは基礎編の程度を越えた問題なので, 詳細は第4部付録に譲るとして, 概略は, まず, 地球楕円体面が1つの等ポテンシャル面であるという条件より, 地球楕円体による重力ポテンシャルU が求まり, その勾配をとることにより, 地球楕円体の重力, すなわち正規重力を与える次式が得られる.
\[ \gamma = \frac{(a\gamma_e \cos^2 \psi + b\gamma_p \sin^2 \psi)}{\sqrt{a^2\cos^2\psi+b^2\sin^2\psi}} \tag{9} \]
ここで, $a$は地球の赤道半径($6,378,137[m]$), $b$ は極半径($6,356,752[m]$), $\gamma _e$は赤道における正規重力($978.032677[Gal]$), $\gamma _p$は極における正規重力($983.218637[Gal]$)であり, この式を正規重力式と呼ぶ. この式を用いてある測地緯度$\psi$ での地球の標準的な重力値が得られるので, 実測された重力値からその値を差し引くことで, 重力異常が計算される.
測地基準系1980での正規重力を表わす重力式1980の展開形としてチェビシェフ近似による,
\[ \gamma = 978.03267715(1+0.0052790414 \sin^2 \psi + 0.0000232718 \sin^4 \psi \\ + 0.0000001262 \sin^6 \psi + 0.0000000007 \sin^8 \psi) \]
がよく用いられる. この式の誤差は, $0.1[\mu Gal]$である.
2-2-2. 重力とジオイド(*)
地球の形を近似するジオイドは, 平均海面に極めて近い重力の等ポテンシャル面と考えられるが, このことのもう少し厳密な定義を与えよう.
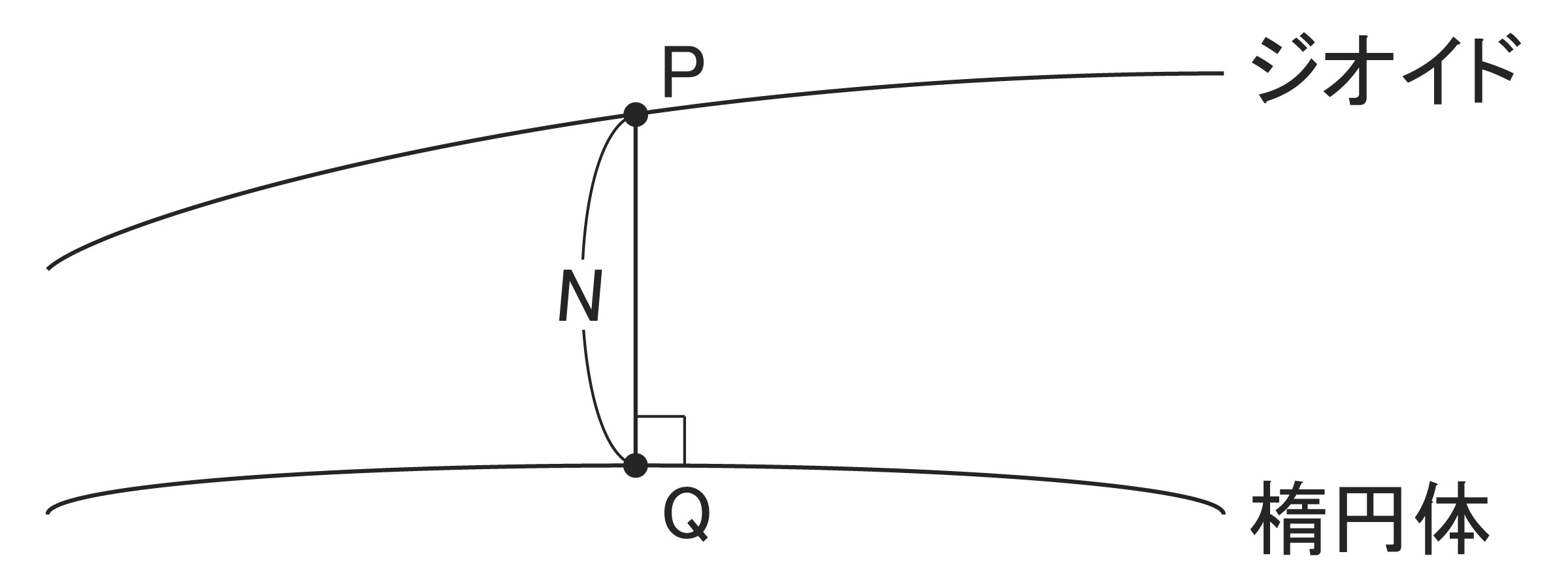
ある測地座標系を記述する地球楕円体(これを正規楕円体と呼ぶ)面は, その楕円体がつくる重力ポテンシャル$U$の1つの等ポテンシャル面であり, それを$U_0$で表す. 一方, 地球の重力ポテンシャルW の等ポテンシャル面は無数にあるが, そのうち, $W=U_0$となる面はただ1つであり, これをジオイドと定義する. すなわち, 地球楕円体が与えられるとそれに対応するジオイドが決まることになり, これは, 数学的に大変明快である. しかし, 地球楕円体のさまざまなパラメーターを決めるのは, 測地学的な計測によるということを忘れてはならない. ジオイドを定義するのも, 地球の形を記述する1つの手段ということである.
さて, もしジオイドが正規楕円体と完全に一致したとすると, ジオイド上での重力ポテンシャル$W$と楕円体のポテンシャル$U$はすべての点で一致して, $U=W=U_0$となるはずである. しかし, 一般に, ジオイドと楕円体とは完全には一致せず, その差がジオイド高$N$である. ジオイド上では, 常に$W=U_0$であるが, ジオイド高$N=0$でなければ, $U$は$U_0$とはならない. $W$と$U$の差,
\[ T=W-U \tag{10} \]
は, 重力乱れポテンシャルと呼ばれているが, 以上の議論から推測できるように, $T$はジオイド高$N$に比例しており, その比例関係は, $\gamma$を楕円体の正規重力として, ブルンズの公式
\[ T=N \gamma \tag{11} \]
で与えられる.
地球楕円体と比べてジオイドに起伏ができるのは, 地球の地形に凹凸があったり, 地球内部の密度分布が均質ではなかったりするためである. 例えば, 図3に示すように地下に質量の大きい物質がある場合を考える. この場合, 物質の引力により重力の方向が内側を向くことになる. 一方, ジオイドは, 重力の方向と垂直な面であるので, 岩石の上では周囲よりも盛りあがる. つまり, 地下に大きな質量があると, その上では重力は大きく, ジオイドも高くなる.
このように, ジオイドの形は重力の分布で決まるものであり, 実際, ジオイド高は, 後述する重力異常をストークス積分することにより計算できる. 宇宙測地技術が利用できるようになるまでは, ジオイド高を直接測定することは不可能であった. 重力異常からいかにしてジオイド高を求めるかは, 現在でも, 測地学の最も基本的かつ重要な課題の1つである.
図3. ジオイドの起伏と地下質量構造.
2-2-3. 重力異常(*)
重力乱れポテンシャル$T$はジオイドの重力ポテンシャル$W$と楕円体のポテンシャル(正規重力ポテンシャル)$U$の差として定義された. 同様に, ジオイド上での点Pでの重力$g_P$と正規重力$\gamma_P$の差
\[ \delta g = g_P - \gamma_P \tag{12} \]
-を重力乱れと呼ぶ(図4). ところで, 重力$g_P$は, 一般には地表の測定点で測られるが, 測定点のジオイドからの距離, すなわち, 標高(正確には正標高)がわかっていれば, 重力の鉛直勾配を補正することでジオイド上での重力値を計算することができる. 一方, 楕円体上での正規重力$\gamma_Q$は計算できるが, ジオイド上での正規重力$\gamma_P$を計算するためには, 楕円体からジオイドまでの距離であるジオイド高$N$が必要であり, $N$は未知量であるので(注)$\gamma_P$を計算することはできない. すなわち, 重力乱れ$\delta g$は測定不可能な量であり, 測定可能なのは, 重力異常と呼ばれるジオイド上での$g_P$と楕円体上での正規重力$\gamma_Q$の差
\[ \Delta g = g_P - \gamma_Q \tag{13} \]
である.
このように定義された重力異常$\Delta g$が地球上のいたるところで得られたとすると, ある点におけるジオイド高$N$は, ストークス積分
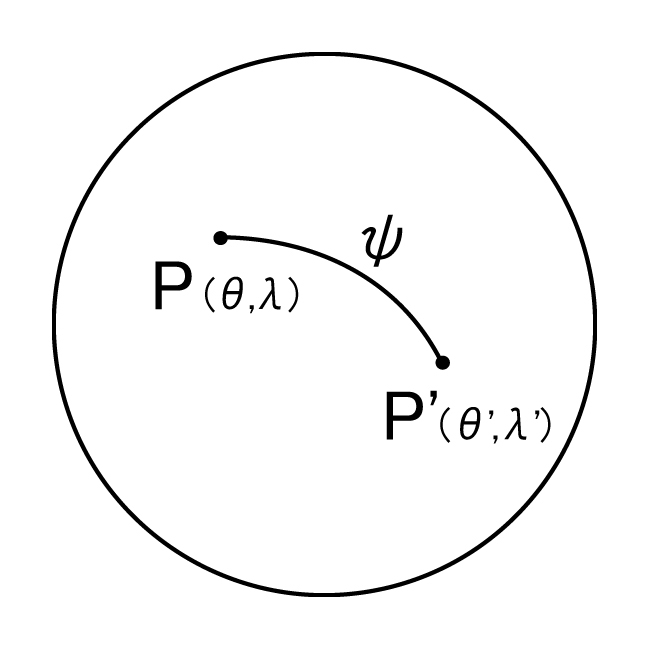
\[ N(\theta,\lambda)=\frac{R}{4\pi\gamma}\iint_\sigma\Delta g(\theta',\lambda')S(\psi)ds' \tag{14} \]
によって計算できることが知られている(詳細は第4部付録, 図5). ここで重要なことは, 重力異常とジオイドの起伏が同じ原因によるということである. 重力異常からジオイド高を求めることは物理測地学の中心課題であり, 現在でも, 高精度なジオイド高を求めるためにさまざまな研究がなされている.
なお, ここでいう重力異常は, 地球物理学で用いられるフリーエア異常とほぼ同じものと理解すればよい. 一方, ブーゲー異常は, 主に地下密度構造の研究に用いる概念であり, フリーエア異常から, ジオイド(あるいはより一般的には探査の対象とする基準面)より上部の質量異常の影響を除いたものである.
図4. ジオイドと楕円体の位置関係と, ジオイド高.
図5. $P(\theta,\lambda)$のジオイド高は, 座標$(\theta',\lambda')$における重力異常$\Delta g(\theta',\lambda')$と, 角距離$\psi$ の関数であるストークス関数$S(\psi)$との積を, 全球積分することによって得られる.
(注)現在では宇宙測地技術で$N$も直接測定できるようになっている.
2-2-3-1. 正標高と正規高(**)
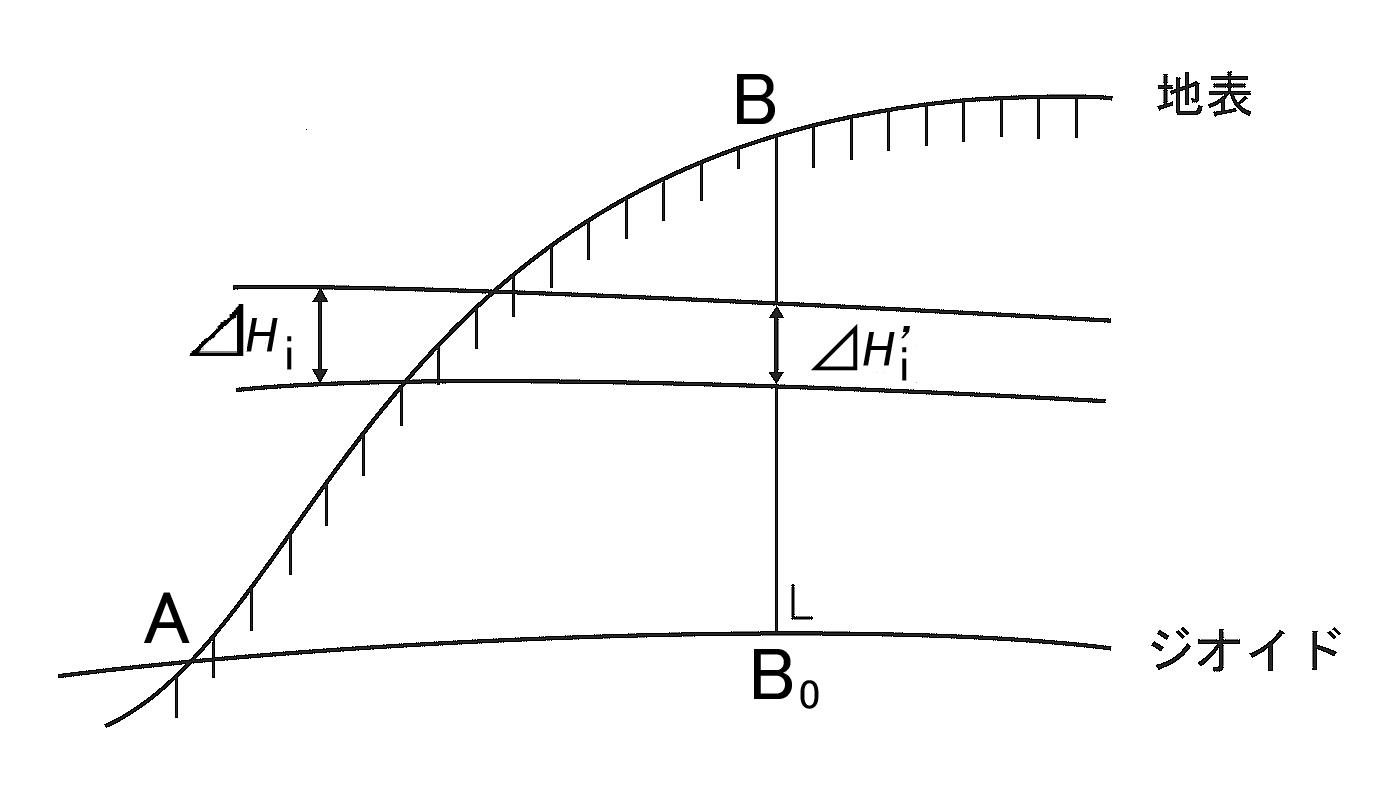
水準測量によって測られた2地点の高さの差は比高と呼ばれる. 水準測量では地表での水準面(重力の等ポテンシャル面)に沿って高さの差を測っていくために, 水準面が平行でない場合には, 比高は測量の経路により異なった値を持つ. 例えば, A点から出発してB点に向かう場合, $AB$の経路をとる場合と$AB_0B$の経路では, 比高は一般に異なった値となる(図6). すなわち,
\[ \sum_{A \rightarrow B}\Delta H_n \neq \sum_{A \rightarrow B_0 \rightarrow B}\Delta H_n \tag{15} \]
であり, ある点の高さを定義するのに, 比高そのものを用いることはできない. そこで, 各測定毎の比高$\Delta H n$にその点での重力$g_n$を掛けたものを足し合わせ, 重力ポテンシャル数と呼ばれる重力ポテンシャルの差,
\[ W=-\sum\Delta H_n \cdot g_n \tag{16} \]
を考える. $W$は保存量であるので, 経路によらず一定の値となり好都合である.
ところで, 重力ポテンシャル数は, 長さの次元を持たないため日常生活で高さとして用いるには不便である. 地表の高さは, 一般にジオイドからの高さで表されるので, 点Bでの重力ポテンシャル数を, BB0間の平均の重力g で割ったものをB点の高さとして用いるのが好都合である. このようにして定義された高さ
\[ H_{ortho}=\frac{1}{\overline{g}}\sum \Delta H_n \cdot g_n \tag{17} \]
を正標高(Orthometric Height)と呼ぶ.
一方, $BB_0$間の平均の重力$g$ は, その付近の密度構造により異なるため, 地表での重力測定値だけからは正確に求まらず, 地下の密度の仮定を必要とする. このため, 平均重力の替わりに理論的に計算可能なBB0間の正規重力の平均値$\gamma$ を用いて定義した,
\[ H_{normal}=\frac{1}{\overline{\gamma}}\sum \Delta H_n \cdot g_n \tag{18} \]
を正規高(Normal Height)と呼ぶ.
我が国で用いられている高さは, 正標高であり, 単に標高と呼ばれている.
図6. 重力の等ポテンシャル面と標高.
2-2-3-2. フリーエア異常(**)
地表での重力測定値を用いて重力異常を計算する際には, 次式に示すように, 重力の鉛直勾配$dg/dz$と正標高から, ジオイド上での重力値を計算し, その後, 楕円体上での正規重力値を差し引くことになる.
\[ \Delta g = g + \left( \frac{dg}{dz} \right)h-\gamma \tag{19} \]
このうち, 重力の鉛直勾配$dg/dz$が場所により異なるため, 代わりに, 正規重力の鉛直勾配である$d\gamma/dz(=0.3086 [mGal/m])$を用いると次式となる.
\[ \begin{eqnarray} \Delta g = \Delta g_F &=& g+ \left( \frac{d\gamma}{dz} \right)h -\gamma \\ &=& g+0.3086h-\gamma \end{eqnarray} \tag{20} \]
地球物理学では, このような高さの補正をフリーエア補正, 計算された重力異常をフリーエア異常$\Delta g F$と呼んでいる.
フリーエア異常では, 重力値の緯度による影響の補正と, 高さ(地球の中心からの距離)の影響の補正はなされているが, 地形や地球内部の密度の違いによる補正は一切されていない. 従って, フリーエア異常には, 地形を含め, 楕円体からの差として, 地球内部の質量分布の情報が, すべて反映されている.
ところで, (18)式の右辺を$-(\gamma-(d\gamma/dz)h)$と書き改めると, 括弧内は, 楕円体からの高さh の点での正規重力を与える. ここで, 高さ$h$として正規高を用いると, 楕円体から正規高$h$ にある軌跡は, 図7に示すようにテルロイドと呼ばれており, 括弧内は, テルロイド上の点$Q$での正規重力となる. 測地学でいうフリーエア異常は, このように定義された地表の重力値とテルロイド上での正規重力との差のことである. 重力異常からジオイド高を求めるのと同様に, フリーエア異常から高度異常(Height anomaly)と呼ばれる地表面とテルロイドの差を計算することができる.
図7. ジオイドとテルロイド.
2-2-3-3. ブーゲー異常(**)
地上での重力測定値を基にフリーエア異常を求めると, 標高の高いところほど大きく, 標高が低い所で小さくなる傾向がある. これは, フリーエア異常には地形による質量の過不足が強く反映されることを意味している. このため, 地下(あるいはある基準面)より下の密度構造を調べるためには, それより上部の物質の影響を計算で取り除き, 基準面より下の質量異常, あるいは密度の大小を反映した重力異常を用いればよい. このような考えで, ジオイドより上の影響を取り除いた重力異常をブーゲー異常と呼ぶ.
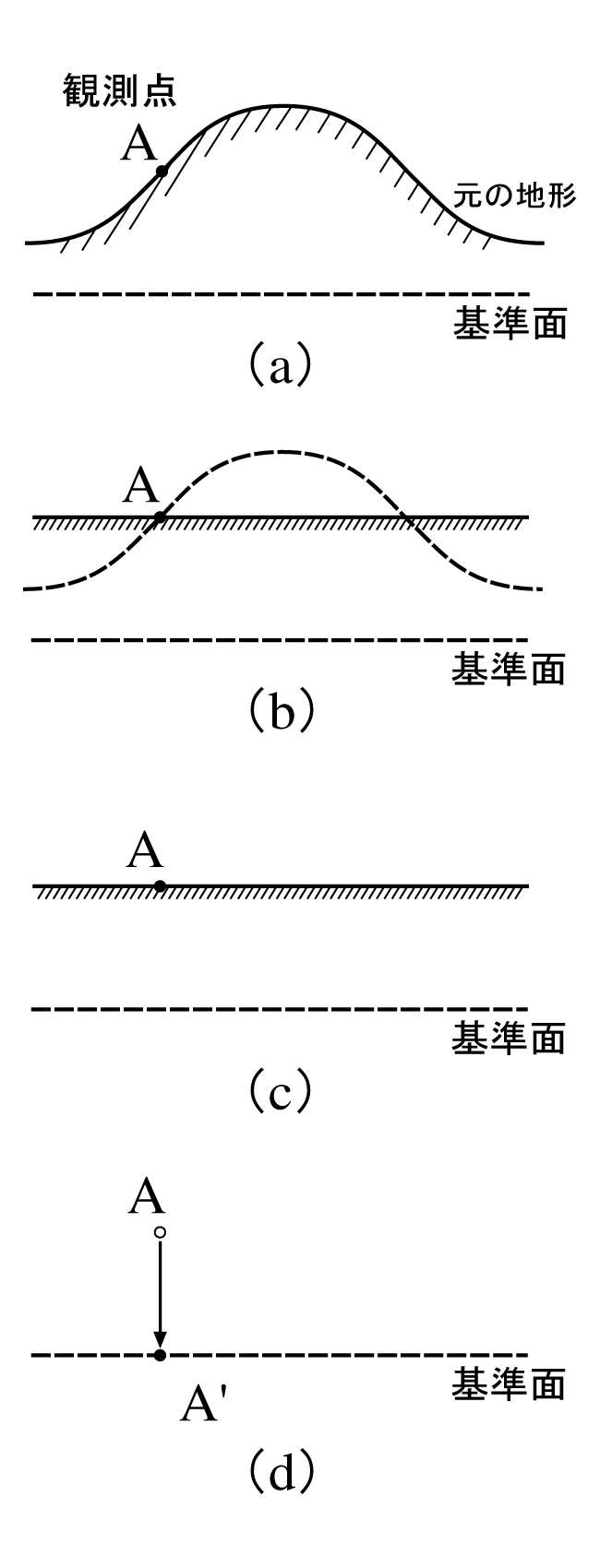
標高$h$の点で, フリーエア異常からブーゲー異常を計算するには, 通常, 地形の起伏の影響を取り除く地形補正と, 地形のならされた密度$\rho_r$と厚さ$h$の無限平板の影響($2\pi G_{\rho_r h}$)を取り除くブーゲー補正を施せばよい. これらをまとめ, 地形補正を$\rho rT$($T$は岩石密度を1としたときの地形補正量)とすると, ブーゲー異常$\Delta gB$は,
\[ \Delta g_B=\Delta g_F -2\pi G\rho _rh +\rho_rT \tag{21} \]
となる(図8). なお, (2-19)式で, 地形補正$ρ_rT$ を省略した場合を単純ブーゲー異常, 地形補正$\rho_rT$ を含めたものを完全ブーゲー異常と呼んで区別することがある.
以上は陸上の場合であるが, 海洋でのブーゲー異常の計算は, 海水を岩石で置き換えることになり, やや複雑である. 厳密には, 海底地形による地形補正を考慮する必要があるが, 簡単に, 海水を密度$\rho_r$の無限平板で置き換える単純ブーゲー異常を考えると, 海の深さを$d$, 海水の密度を$\rho_w$として,
\[ \Delta g_B =\Delta g_F + 2\pi G(\rho_r - \rho_\omega)d \tag{22} \]
で与えられる.
図8. (a)実際の観測条件 . (b)地形補正を加えて, 平らな地盤上の重力値に直す. (c)ブーゲー補正を加えて, 基準面より上部の物質の影響を除く. (d)フリーエア補正により, 基準面での重力値を求める.
2-2-3-4. ブーゲー異常と地下構造(**)
地下に周囲より密度の大きい物体があれば, その上で, ブーゲー異常は大きくなる. このことは, 堆積層で覆われた基盤構造の決定, 褶曲構造, 潜在断層, カルデラ構造の検出などに利用されている. ブーゲー異常を用いたこのような地下構造探査は, 重力探査と呼ばれている. 以下にその例を示す.
厚い地層が堆積している場合, 一般に下の地層ほど古く密度が大きくなる. このような地層が褶曲すると, 背斜の部分では高密度の下部地層が地表に近づくためブーゲー異常が大きくなり, 逆に向斜の部分ではブーゲー異常が小さくなる. 石油や天然ガスは, 背斜の部分に溜るので, ブーゲー異常による褶曲構造の調査は資源探査にも利用される. 第2次世界大戦後の重力測定や重力探査の著しい進歩は, 実は, このような石油探査を目的としたものであった(図9).
沖積平野では, 地表面は平らでもその基盤構造には起伏があり, 沖積層の厚さが場所により変化していることがよくある. 一般に沖積層の密度は基盤岩に比べて小さいため, ブーゲー異常は基盤地形と大変よく似た形状を示す. 沖積層の厚いところでは, 地盤が軟弱で地震のときに大きな被害を受ける可能性があるが, ブーゲー異常からこのような地域を予想することも可能である.
重力探査は, 地下の断層構造の研究にも利用されている. 基盤の表面に上下に大きな段差をもつ縦ずれ断層では, 断層を境として地下の密度分布に差が生じるため, 断層の真上でブーゲー異常に急激な変化がみられる. この変化は, 正断層では地表の断層露頭よりも下盤側で, また, 逆断層では上盤側で大きくなるので, 断層の傾斜を推定することができ, また, ブーゲー異常の変化量からずれの量を見積もることも可能である(図10).
重力探査は, 火山調査にも有効である. とくに地下の物質が大量に噴出し, 上の山体が落ち込んでできたカルデラは, 非常にきれいな同心円状の負の異常を示すことが知られている. これは落ちた山体が粉々になり, 周囲の岩石よりも密度が小さくなるためである. ただ, 例外もあり, 伊豆大島三原山は負の異常を示さない.
図9. 背斜構造とブーゲー異常.
図10. 基盤構造とブーゲー異常.
2-2-3-5. アイソスタシー(**)
今から200年ほど前, インドのヒマラヤ山脈の麓で垂直線偏差の測定がなされた. ヒマラヤの山体の引力により, ヒマラヤの麓では20''程度の垂直線偏差が測定されると期待された. しかし実際に測定してみると, それはわずか3''程度であり, これを説明するのに考え出されたのがアイソスタシー説である. この説によると, ヒマラヤのような大きな山体は, その分だけ周りより密度の小さい根を持っており, 逆に, 深い海洋の海洋地殻は, 海水による質量不足分だけ密度が大きいと考えられる. これは, 長い時間スケールではマントルが流動性を有するためで, 水に木片を浮かべるのと同様に, 密度の小さい大陸や山体が密度の大きい岩石の上に浮かんでいると考えればよい.
アイソスタシーのモデルとして, 初期には, 密度は一定で標高の高いところほど根が深くなるエアリー・ハイスカーネンのモデル(図11)と, 根の深さが一定で標高に応じて密度が変化するプラット・ヘイフォードのモデル(図12)が提唱された. その後, 地震波の伝わり方から, 大陸地殻が厚く, 海洋地殻が薄いことが分かり, エアリー・ハイスカーネンのモデルが現実に近いと考えられた. 一方, プレートテクトニクスの考えによると, 物性的にみて流動性に富むのはリソスフェアではなくアセノスフェアであり, 平らな底面を持つリソスフェアが, アセノスフェアの上に浮かんでいると考える方が自然であり, これはプラット・ヘイフォードのモデルに近い. 最近では, これらのモデルを結合し, 補償面を地殻の底面ではなくリソスフェアとアセノスフェアの境界に取った, 図13のようなモデルが現実に近いと考えられている.
アイソスタシーの概念は, 重力と浮力の上下方向の静的な釣り合いを説明しているに過ぎない. 従って, スカンジナビア半島やカナダのハドソン湾周辺でみられる最終氷期後のアイソスタシーの回復運動(ポストグレーシャルリバウンド:PGR)のように, 現在進行中の動的な現象や, また, 重力や浮力以外の力が作用している場合にはアイソスタシーは成立しない. アイソスタシーは, 空間波長約1000km程度よりも長波長の領域では, よく成り立っていることが知られているが, 波長100km程度よりも短波長の領域では, 一般に, フリーエア異常と地形との相関が大変よくなり, アイソスタシーはほとんど成立していない. このような領域では, 地形による荷重は, 浮力ではなく, 地殻, あるいはリソスフェアの弾性によって支えられるためで, アイソスタシーが成り立つかどうかは, このような地下の弾性的性質を知る手がかりも与えてくれる.

図11. エアリー・ハイスカネンモデル.
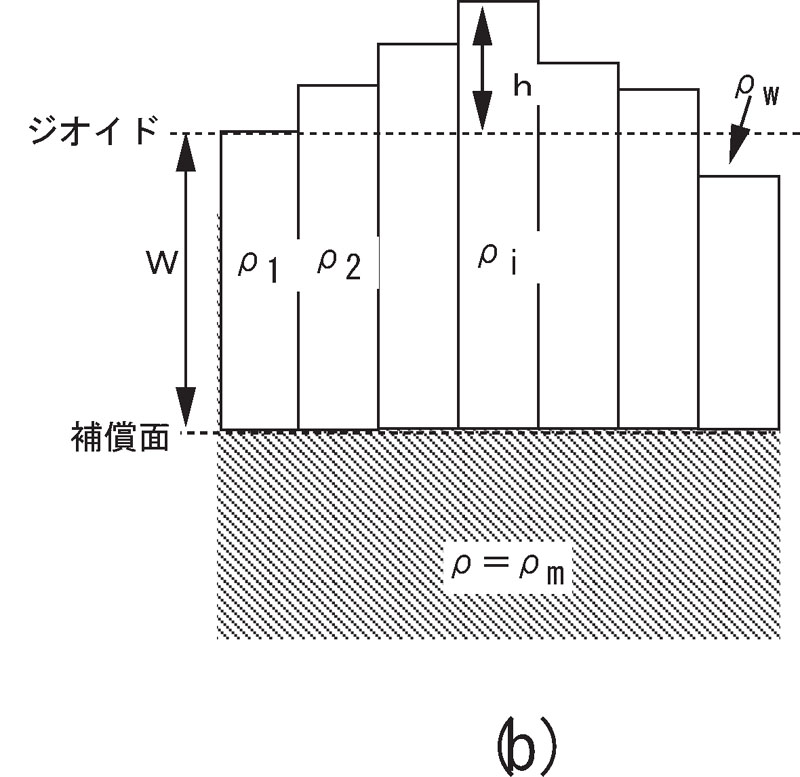
図12. プラット・ヘイフォードモデル.

図13. エアリー・ハイスカネン-プラット・ヘイフォード混合モデル.